Effect of temperature and magnetoelastic loads on the free vibration of a sandwich beam with magnetorheological core and functionally graded material constraining layer

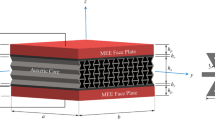
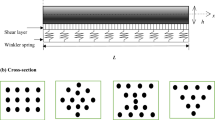
Abstract

In this paper, we investigate the effects of temperature and magnetoelastic load, on the free vibration of an elastomer sandwich beam with magnetorheological (MR) core and functionally graded material (FGM) constraining lamina under high temperature environment. This sandwich beam is named FGMR beam in this paper. The material properties of the functionally graded material layers are assumed to be temperature-dependent and vary continuously through-the-thickness according to a simple power-law distribution in terms of the volume fractions of the constituents. Also, it is assumed that the beam may be clamped, hinged, or free at its ends and is subjected to one-dimensional steady-state heat conduction in the thickness direction. The classical Hamilton’s principle and the assumed mode method are used to set up the equations of motion. The convergence of the method is examined and the accuracy of the results is verified by comparing the results with those available. In fact, the aim of this study is to investigate the effect of some parameters on the dynamic behavior of a sandwich beam with magnetorheological core and FGM constraining layers under temperature environment. First, the effects of magnetic field intensity on natural frequency and modal loss factor of the FGMR beam are studied. Subsequently the influence of temperature distribution on the vibration of FGMR sandwich beam is shown for different boundary condition and volume fraction index. Finally, the effect of the slenderness ratio on the fundamental frequency is presented. The results show that the modal characteristics are significantly influenced by the applied magnetic field, volume fraction index, temperature change, slenderness ratio, and the end support conditions.

Appendix

The coefficients of the potential and kinetic energies of the functionally graded layers;

$$\begin{aligned} {D}_{i}^{1}&={\int }_{-{h}_{i}/2}^{{h}_{i}/2}\left(\frac{{E}_{i}\left({z}_{i},{T}_{i}\right)}{1-{\nu }_{i}^{2}\left({z}_{i},{T}_{i}\right)}\right){\hbox{d}z}_{i} ,\quad i=t, \, b, \\ {D}_{i}^{2}&={\int }_{-{h}_{i}/2}^{{h}_{i}/2}\left(\frac{{E}_{i}\left({z}_{i},{T}_{i}\right)}{1-{\nu }_{i}^{2}\left({z}_{i},{T}_{i}\right)}\right){{z}_{i}\hbox{d}z}_{i} ,\\ {D}_{i}^{3}&={\int }_{-{h}_{i}/2}^{{h}_{i}/2}\left(\frac{{E}_{i}\left({z}_{i},{T}_{i}\right)}{1-{\nu }_{i}^{2}\left({z}_{i},{T}_{i}\right)}\right){{z}_{i}^{2}\hbox{d}z}_{i},\end{aligned}$$

(46)

$$\begin{aligned} {\Lambda }_{i}^{1}&={\int }_{-{h}_{i}/2}^{{h}_{i}/2}\left(-\frac{E\left({z}_{i},{T}_{i}\right)\alpha \left({z}_{i},{T}_{i}\right)}{1-\nu \left({z}_{i},{T}_{i}\right)}\Delta T\left({z}_{i}\right)\right){\hbox{d}z}_{i} ,\quad i=t,b, \\{\Lambda }_{i}^{2}&={\int }_{-{h}_{i}/2}^{{h}_{i}/2}\left(-\frac{E\left({z}_{i},{T}_{i}\right)\alpha \left({z}_{i},{T}_{i}\right)}{1-\nu \left({z}_{i},{T}_{i}\right)}\Delta T\left({z}_{i}\right)\right){{z}_{i}\hbox{d}z}_{i},\\{\Lambda }_{i}^{3}&={\int }_{-{h}_{i}/2}^{{h}_{i}/2}\left(-\frac{E\left({z}_{i},{T}_{i}\right)\alpha \left({z}_{i},{T}_{i}\right)}{1-\nu \left({z}_{i},{T}_{i}\right)}\Delta T\left({z}_{i}\right)\right){{z}_{i}^{2}\hbox{d}z}_{i},\end{aligned}$$

(47)

$$\begin{aligned} {F}_{i}^{1}&={\int }_{-{h}_{i}/2}^{{h}_{i}/2}{\rho }_{i}\left({z}_{i},{T}_{i}\right){\hbox{d}z}_{i} ,\quad i=t, b, c ,\\{F}_{i}^{2}&={\int }_{-{h}_{i}/2}^{{h}_{i}/2}{\rho }_{i}\left({z}_{i},{T}_{i}\right){{z}_{i}\hbox{d}z}_{i} ,\\ {F}_{i}^{3}&={\int }_{-{h}_{i}/2}^{{h}_{i}/2}{\rho }_{i}\left({z}_{i},{T}_{i}\right){{z}_{i}^{2}\hbox{d}z}_{i}.\end{aligned}$$

(48)

The coefficients of the mass matrices for the FGMR beam:

$$\begin{aligned} {{M}}_{11}&=\left(B\left({F}_{{\rm t}}^{3}+{F}_{{\rm b}}^{3}\right)+{\xi }_{1}{S}^{2}\right){\int }_{0}^{L}{\psi }_{i}^{{^{\prime}}}{\psi }_{j}^{{^{\prime}}}\hbox{d}x+\left(B\left({F}_{{\rm t}}^{1}+{F}_{{\rm b}}^{1}\right)+{\xi }_{3}\right){\int }_{0}^{L}{\psi }_{i}{\psi }_{j}\hbox{d}x,\\ {{M}}_{12}&={\xi }_{1}S{\int }_{0}^{L}{\psi }_{i}^{{^{\prime}}}{\varphi }_{j}\hbox{d}x,\\ {{M}}_{13}&=-{\xi }_{1}S{\int }_{0}^{L}{\psi }_{i}^{{^{\prime}}}{\varphi }_{j}\hbox{d}x,\\ {{M}}_{21}&={\xi }_{1}S{\int }_{0}^{L}{\varphi }_{i}{\psi }_{j}^{{^{\prime}}}\hbox{d}x,\\ {{M}}_{22}&=\left(B{F}_{{\rm t}}^{1}+{\xi }_{1}\right){\int }_{0}^{L}{\varphi }_{i}{\varphi }_{j}\hbox{d}x,\\ {{M}}_{23}&=-{\xi }_{1}{\int }_{0}^{L}{\varphi }_{i}{\varphi }_{j}\hbox{d}x,\\ {{M}}_{31}&=-{\xi }_{1}S{\int }_{0}^{L}{\varphi }_{i}{\psi }_{j}^{{^{\prime}}}\hbox{d}x,\\ {{M}}_{32}&=-{\xi }_{1}{\int }_{0}^{L}{\varphi }_{i}{\varphi }_{j}\hbox{d}x,\\ {{M}}_{33}&=\left(B{F}_{{\rm b}}^{1}+{\xi }_{1}\right){\int }_{0}^{L}{\varphi }_{i}{\varphi }_{j}\hbox{d}x.\end{aligned}$$

(49)

The coefficients of the stiffness matrices for the FGMR beam:

$$\begin{aligned} K_{11} &= B\left( {D_{{\rm t}}^{3} + D_{{\rm b}}^{3} + \Lambda_{{\rm t}}^{3} + \Lambda_{{\rm b}}^{3} } \right)\mathop \int \limits_{0}^{L} \psi_{i}^{\prime \prime } \psi_{j}^{\prime \prime } {\text{d}}x + \left( {B\left( {\Lambda_{{\rm t}}^{1} + \Lambda_{{\rm b}}^{1} } \right) + \xi_{2} S^{2} } \right)\mathop \int \limits_{0}^{L} \psi_{i}^{\prime } \psi_{j}^{\prime } {\text{d}}x \\ & \quad - \xi_{8} \mathop \int \limits_{0}^{L} \left( {\ln \frac{1}{L - x}} \right)\psi_{i}^{\prime \prime } \psi_{j}^{\prime } {\text{d}}x + \xi_{9} \mathop \int \limits_{0}^{L} \psi_{i}^{\prime } \psi_{j}^{\prime } {\text{d}}x - \xi_{10} \mathop \int \limits_{0}^{L} \psi_{i}^{\prime \prime \prime} \psi_{j}^{\prime } {\text{d}}x,\\ {K}_{12}&={\xi }_{2}S{\int }_{0}^{L}{\psi }_{i}^{{^{\prime}}}{\varphi }_{j}\hbox{d}x-2B\left({D}_{{\rm t}}^{2}+{\Lambda }_{{\rm t}}^{2}\right){\int }_{0}^{L}{\psi }_{i}^{{^{\prime}}{^{\prime}}}{\varphi }_{j}^{{^{\prime}}}\hbox{d}x,\\{K}_{13}&=-{\xi }_{2}S{\int }_{0}^{L}{\psi }_{i}^{{^{\prime}}}{\varphi }_{j}\hbox{d}x-2B\left({D}_{{\rm b}}^{2}+{\Lambda }_{{\rm b}}^{2}\right){\int }_{0}^{L}{\psi }_{i}^{{^{\prime}}{^{\prime}}}{\varphi }_{j}^{{^{\prime}}}\hbox{d}x,\\{K}_{21}&={\xi }_{2}S{\int }_{0}^{L}{\varphi }_{i}{\psi }_{j}^{{^{\prime}}}\hbox{d}x+{\xi }_{6}{\int }_{0}^{L}{\left(ln\frac{1}{L-x}\right)}^{-1}{\varphi }_{i}^{{^{\prime}}}{\psi }_{j}^{{^{\prime}}}\hbox{d}x,\\ {K}_{22}&=B\left({D}_{{\rm t}}^{1}+{\Lambda }_{{\rm t}}^{1}\right){\int }_{0}^{L}{\varphi }_{i}^{{^{\prime}}}{\varphi }_{j}^{{^{\prime}}}\hbox{d}x+{\xi }_{2}{\int }_{0}^{L}{\varphi }_{i}{\varphi }_{j}\hbox{d}x+{\xi }_{4}{\int }_{0}^{L}{\varphi }_{i}^{{^{\prime}}{^{\prime}}}{\varphi }_{j}\hbox{d}x,\\ {K}_{23}&=-{\xi }_{2}{\int }_{0}^{L}{\varphi }_{i}{\varphi }_{j}\hbox{d}x,\\ {K}_{31}&=-{\xi }_{2}S{\int }_{0}^{L}{\varphi }_{i}{\psi }_{j}^{{^{\prime}}}\hbox{d}x+{\xi }_{7}{\int }_{0}^{L}{\left(ln\frac{1}{L-x}\right)}^{-1}{\varphi }_{i}^{{^{\prime}}}{\psi }_{j}^{{^{\prime}}}\hbox{d}x,\\ {K}_{32}&=-{\xi }_{2}{\int }_{0}^{L}{\varphi }_{i}{\varphi }_{j}\hbox{d}x,\\ {K}_{33}&=B\left({D}_{{\rm b}}^{1}+{\Lambda }_{{\rm b}}^{1}\right){\int }_{0}^{L}{\varphi }_{i}^{{^{\prime}}}{\varphi }_{j}^{{^{\prime}}}\hbox{d}x+{\xi }_{2}{\int }_{0}^{L}{\varphi }_{i}{\varphi }_{j}\hbox{d}x+{\xi }_{5}{\int }_{0}^{L}{\varphi }_{i}^{{^{\prime}}{^{\prime}}}{\varphi }_{j}\hbox{d}x.\end{aligned}$$

(50)

where

$$\begin{aligned} {\xi }_{1}&=\frac{{\rho }_{{\rm c}}{I}_{{\rm c}}}{{h}_{{\rm c}}^{2}} ,\quad {\xi }_{2}=\frac{{G}_{{\rm c}}^{*}{A}_{{\rm c}}}{{h}_{{\rm c}}^{2}} ,\quad {\xi }_{3}={\rho }_{{\rm c}}{A}_{{\rm c}} ,\quad {\xi }_{4}=\frac{{B}_{0}^{2}B{h}_{{\rm t}}}{{\mu }_{et}} ,\quad {\xi }_{5}=\frac{{B}_{0}^{2}B{h}_{{\rm b}}}{{\mu }_{eb}} ,\quad {\xi }_{6}=\frac{{\pi B}_{0}^{2}B{h}_{{\rm t}}}{2{\mu }_{0}},\\ {\xi }_{7}&=\frac{{\pi B}_{0}^{2}B{h}_{{\rm b}}}{2{\mu }_{0}} ,\quad {\xi }_{8}=\frac{{B}_{0}^{2}B\left({h}_{{\rm b}}^{2}+{h}_{{\rm t}}^{2}\right)}{2\pi {\mu }_{0}} ,\quad {\xi }_{9}=\frac{{B}_{0}^{2}B\left({h}_{{\rm b}}+{h}_{{\rm b}}\right)}{{\mu }_{0}} ,\quad {\xi }_{10}=\frac{{B}_{0}^{2}B}{12}\left(\frac{{h}_{{\rm b}}^{3}}{{\mu }_{eb}}+\frac{{h}_{{\rm t}}^{3}}{{\mu }_{et}}\right).\end{aligned}$$

(51)